Understanding the GeLU Fusion with TF-Grappler Visualization Tool

Introduction

This post focuses on the GELU activation and showcases a debugging tool I created to visualize the TF op graphs. The Gaussian Error Linear Unit, or GELU, is an activation function widely used in Transformer based models. It usually comes in with one of the two forms: exact or approximate:

• Exact form:
• Approximate form:

Using GELU is pretty simply in the mainstream Deep Learning frameworks. For example, in Tensorflow, users can call tf.nn.gelu(x, approximate=True) for the approximate GELU over the tensor x. In this post, we will investigate what will happen under the hood after the call and how CPU/GPU is going to optimize this operation.

Visualizing Op Graph Optimized by TF Grappler

For me, the GELU function is quite exotic and not like other activation functions, such as RELU. The computation overhead of GELU is also much larger considering it is composed of many ops, e.g., addition, multiplication, tanh, erf, etc. Essentially, all these operations are pointwise operations and fortunately, the DL framework is able to fuse them as a single operasion (or less operations) by some graph optimization techniques. In TF, this is done via the TF grappler remapping pass. To better understand what patterns are matched, I created this visualizing tool to print out op graphs before and after any specified grappler optimization pass. Please check out the sample scripts in the repo which include the GELU examples and how to generate the graph pictures.

Approximate GELU Pattern

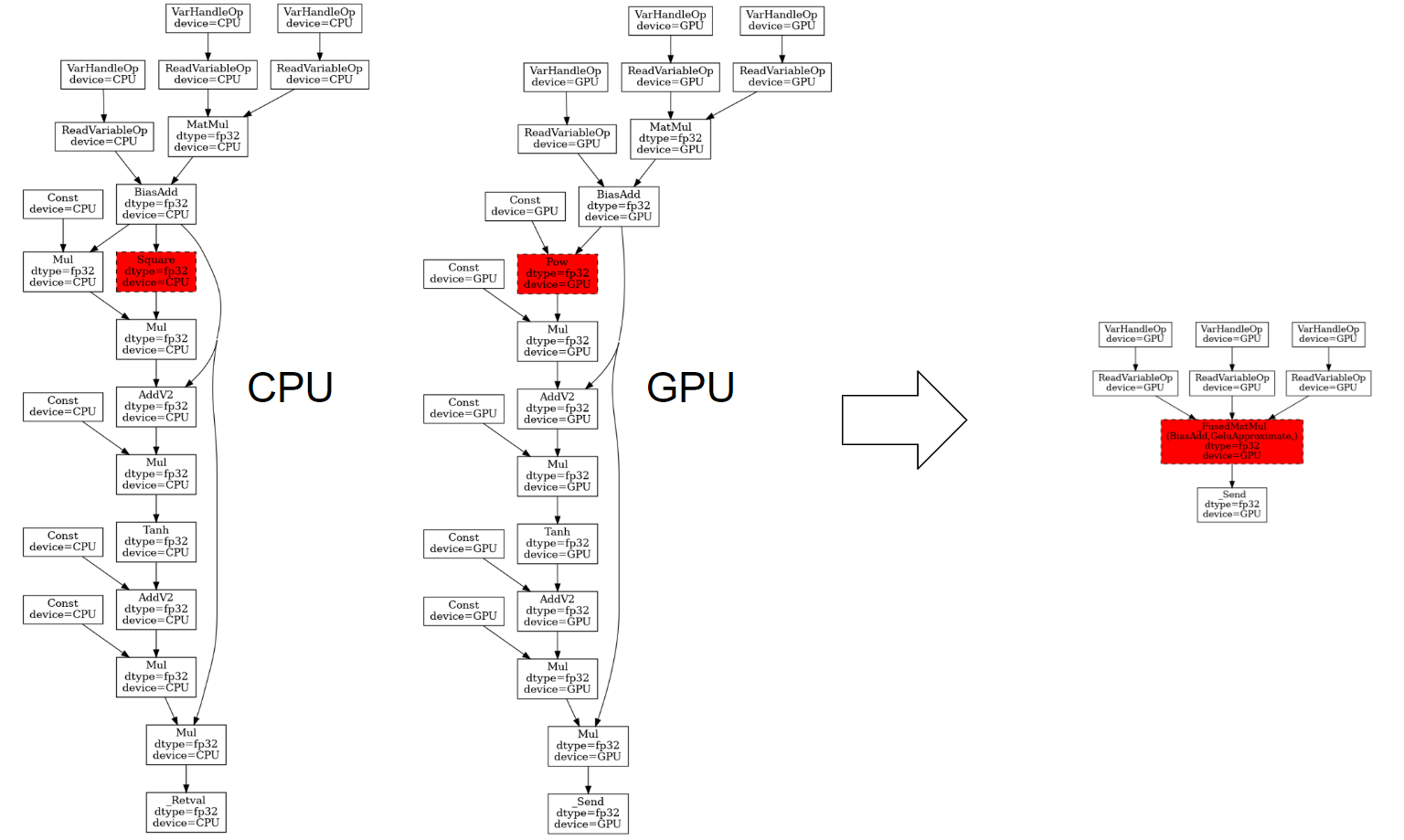
The following figures show the actual op graphs of MatMul->BiasAdd->GELU on GPU and CPU. As we can see from the left-hand side (i.e. before remapping optimization), there is actually no single op named GELU, but a bunch of Mul, AddV2, etc. following the MatMul and BiasAdd.

It is worth noting the op graphs are a bit different on CPU and GPU for the approximate GELU. In particular, CPU computes the x^3 by using mul(square(x), x), while GPU simply calls pow(x, 3). This is actually done by the arithmetic optimization (yeah, another grappler pass) probably because on CPUs, the square() is much faster than the pow(). Whereas on GPUs, we would like to save the device memory round-trip by calling a single op instead of multiple ops.

In TF, both of above GELU patterns can be recognized and fused with the preceding MatMul and BiasAdd by the grappler remapper. Under the hood, the remapper conducts a DFS traversal to find a match from the root node (Mul) of the pattern and the current node of the graph and recursively matches children subpatterns and the children of current node. On the right-hand side of the figure (i.e. after remapping optimization), we see a much clearer graph with basically only one _FusedMatMul node. This can greatly improve the graph execution performance by reducing the kernel launch and memory access overhead. To enable this behavior, we need to turn on the cuBLASLt library (TF_USE_CUBLASLT=1) on GPUs or use the MKL library on CPUs.

Fig 1. GELU Approximate Pattern Fusion

Exact GELU Pattern

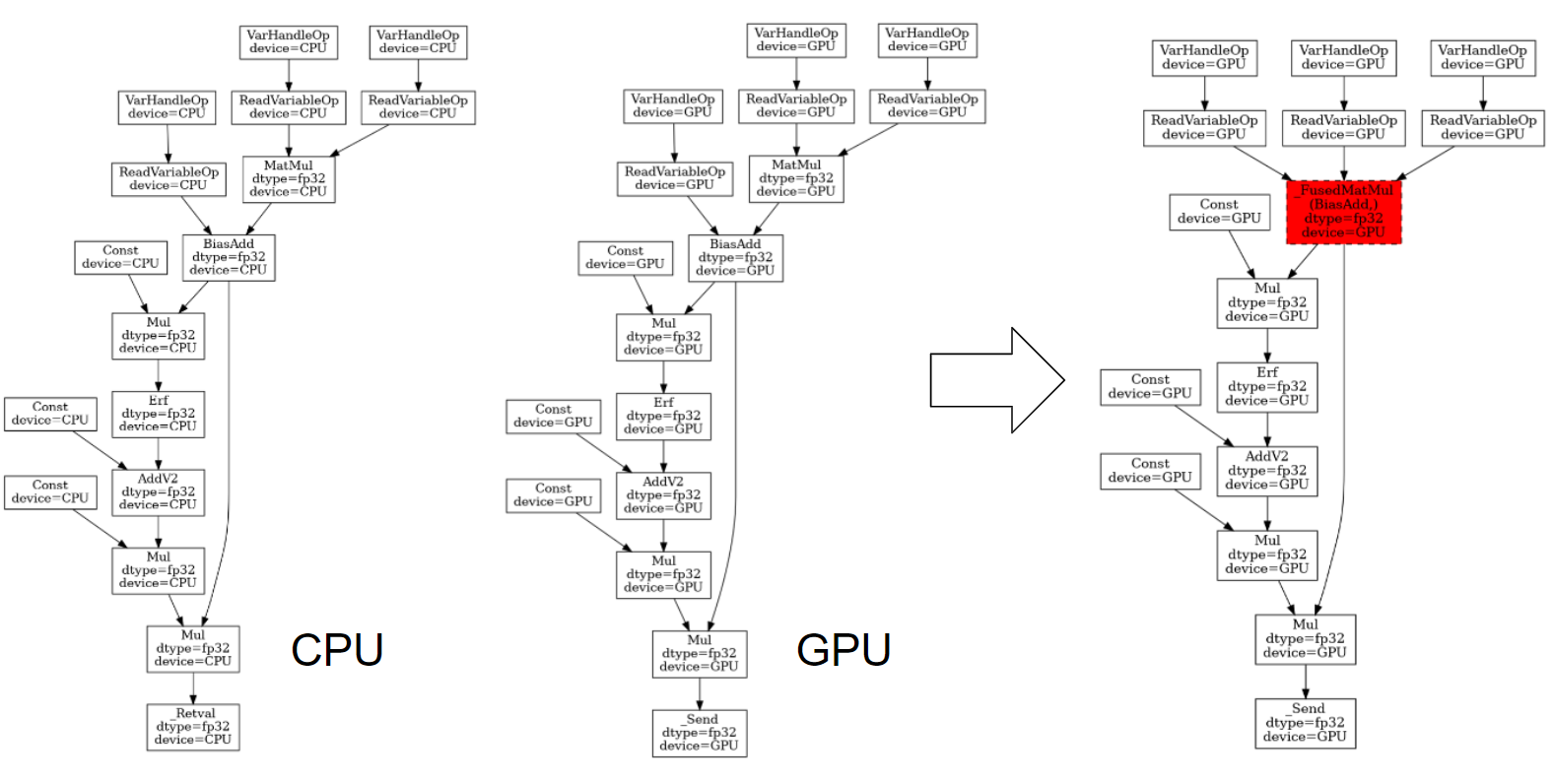
The op graphs of the exact GELU are same on CPU and GPU. Unfortunately, cuBLASLt doesn’t support this form of GELU at this point, so the TF can only fuse the MatMul and BiasAdd as a single op _FusedMatMul. In comparison, the MKL is able to recognize the exact GELU and replace all of them as a single op like in the case of the approximate GELU.

Fig 2. GELU Exact Pattern Fusion

• 2022 3
• 2021 8
• 2020 1